< 금광 >
[문제]
n x m 크기의 금광이 있다. 금광은 1 x 1 크기의 칸으로 나누어져 있으며, 각 칸은 특정한 크기의 금이 들어 있다. 채굴자는 첫 번째 열부터 출발하여 금을 캐기 시작한다. 맨 처음에는 첫 번째 열의 어느 행에서든 출발할 수 있다. 이후에 m번에 걸쳐서 매번 오른쪽 위, 오른쪽, 오른쪽 아래 3가지 중 하나의 위치로 이동해야 한다. 결과적으로 채굴자가 얻을 수 있는 금의 최대 크기를 출력해라. 만약 다음과 같이 3 x 4 크기의 금광이 존재한다고 가정하자.
[입력]
- 첫째 줄에 테스트 케이스 T가 입력된다.(1 <= T <= 1,000)
- 매 테스트 케이스 첫째 줄에 n과 m이 공백으로 구분되어 주어진다.(1 <= n, m <= 20) 둘째 줄에 n x m개의 위치에 매장된 금의 개수가 공백으로 구분되어 입력된다.(1 <= 각 위치에 매장된 금의 개수 <= 100)
[출력]
- 테스트 케이스마다 채굴자가 얻을 수 있는 금의 최대 크기를 출력한다. 각 테스트 케이스는 줄 바꿈을 이용해 구분한다.
| 예제 입력 | 예제 출력 |
| 2 3 4 1 3 3 2 2 1 4 1 0 6 4 7 4 4 1 3 1 5 2 2 4 1 5 0 2 3 0 6 1 2 |
19 16 |
아이디어
이차원배열 dp를 만든다. dp의 i행 j열에는 금광의 i행 j열까지 왔을 때의 최대 금괴의 개수를 저장한다.
풀이 및 코드
# 완성된 dp를 이용해 마지막열의 최댓값을 리턴
def seekAnswer(dp):
maximum = 0
for row in dp:
maximum = max(maximum, row[-1])
return maximum
# 입력을 받고 이중배열 board를 만들어줌
def makeBoard():
tmp = list(map(int, input().split()))
board = [[] for _ in range(n)]
for i in range(n):
for j in range(m):
board[i].append(tmp[i * m + j])
return board
for _ in range(int(input())):
n, m = map(int, input().split())
board = makeBoard()
# dp[row][col]에는 이전 열의 인접한 dp칸들 중 가장 큰 값 + board[row][col]
dp = [[0 for _ in range(m)] for _ in range(n)]
# dp의 각 행의 0번 인덱스에 금광의 1열 입력
for row in range(n):
dp[row][0] = board[row][0]
for col in range(1, m):
for row in range(n):
dp[row][col] = dp[row][col - 1] + board[row][col]
# 인덱스에러 방지용 조건
if (row != 0):
dp[row][col] = max(dp[row][col], dp[row - 1][col - 1] + board[row][col])
# 인덱스에러 방지용 조건
if (row != n - 1):
dp[row][col] = max(dp[row][col], dp[row + 1][col - 1] + board[row][col])
print(seekAnswer(dp))아래는 나동빈님의 코드이다.
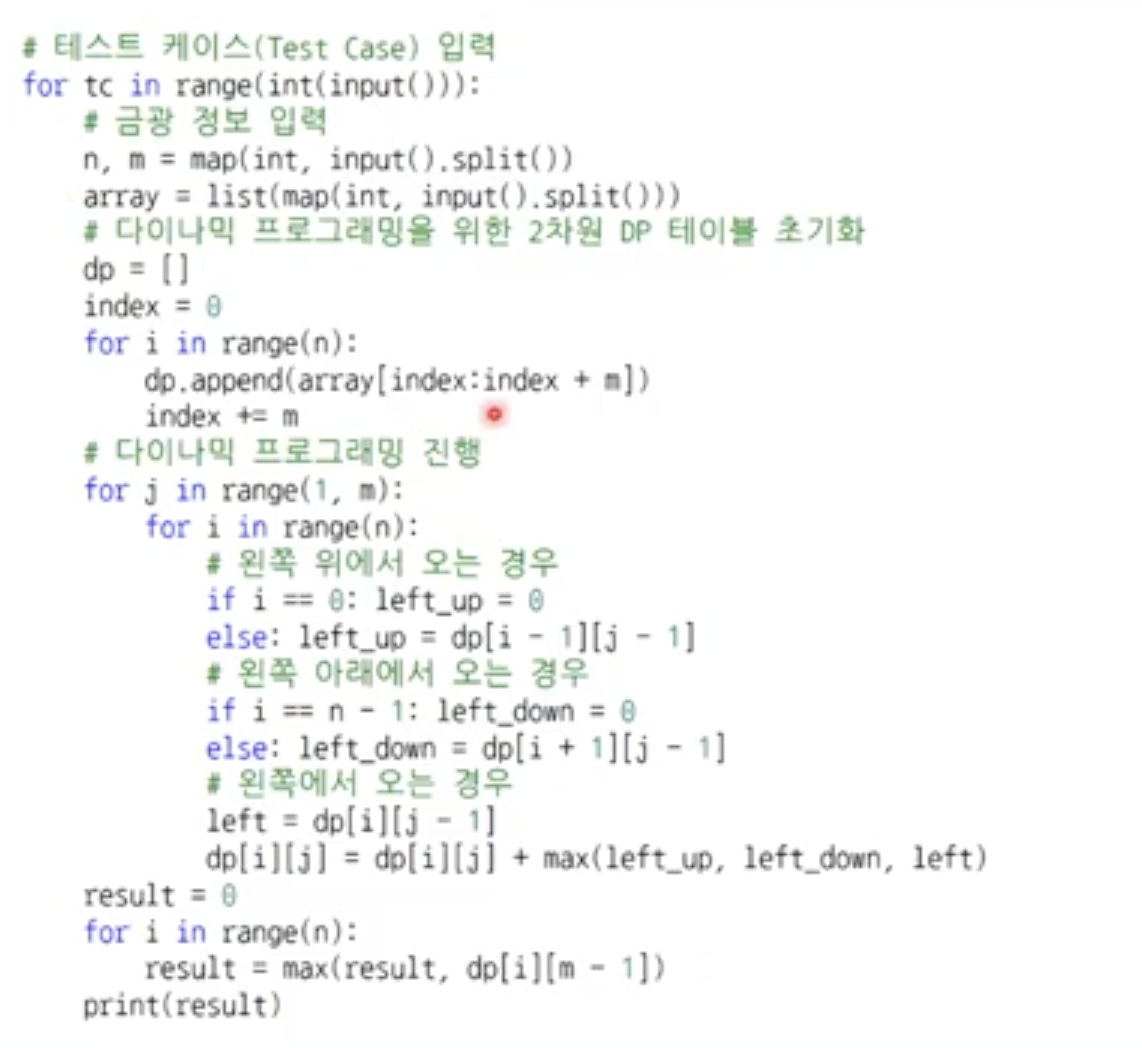
자세히 보면 나와는 다르게 board 배열은 없고, dp를 board로 사용한다. 이처럼 dp의 값을 갱신할 때 원래 dp안에 들어있는 값을 이용할 수도 있다.
후기
dp는 이차원배열로도 만들 수 있다.
'공부 > 이것이 코딩테스트다' 카테고리의 다른 글
| 다이나믹 프로그래밍 - 효율적인 화폐 구성 (0) | 2023.02.22 |
|---|---|
| 다이나믹 프로그래밍 - 1로 만들기 (0) | 2023.02.22 |
| 다이나믹 프로그래밍 - 개미전사 (2) | 2023.02.21 |
| 다이나믹 프로그래밍 이론 (0) | 2023.02.21 |
| 이진 탐색 - 정렬된 배열에서 특정 수의 개수 구하기 (0) | 2023.02.14 |
