정답 코드 및 풀이는 맨 아래에 있습니다.
https://www.acmicpc.net/problem/1300
- '의외로 이분 탐색으로 풀 수 있는 놀라운 문제 1'라고 설명되는 문제이다. 실제로 그랬다.
- 구상이 상당히 어려웠다. 처음 보았을 땐 이분탐색 알고리즘으로 푸는 방법이 전혀 생각나지 않았다. 구상이 어려워 다른 풀이를 조금 참고하여 풀었다.
< K번째 수 >
[문제]
세준이는 크기가 N×N인 배열 A를 만들었다. 배열에 들어있는 수 A[i][j] = i×j 이다. 이 수를 일차원 배열 B에 넣으면 B의 크기는 N×N이 된다. B를 오름차순 정렬했을 때, B[k]를 구해보자.
배열 A와 B의 인덱스는 1부터 시작한다.
[입력]
첫째 줄에 배열의 크기 N이 주어진다. N은 10^5보다 작거나 같은 자연수이다. 둘째 줄에 k가 주어진다. k는 min(10^9, N^2)보다 작거나 같은 자연수이다.
[출력]
B[k]를 출력한다.
| 예제 입력 | 예제 출력 |
| 3 7 |
6 |

이를 배열 B에 넣으면 [1, 2, 2, 3, 3, 4, 6, 6, 9]이다. B[7] = 6이다.(배열의 시작 인덱스는 1 임)
아이디어
N은 최대 10^5이므로 배열을 직접 만든다면 10^10 크기의 배열을 만들어야 한다. 정수를 넣어야 하기 때문에 각 원소당 4Byte라고 하면, 40Gb의 크기가 필요하므로 제한에 걸리게 된다. 따라서 배열의 크기 N을 이용해서 특정 숫자의 순서가 몇 번째인지를 알 수 있는 알고리즘을 짜야한다. 이 부분이 상당히 어려웠고, 거듭 고민하다 다른 사람의 풀이를 참고하였다. 수학을 이용하면 생각보다 쉽게 짤 수 있었다.
그 방법은 타겟 숫자를 각 행(혹은 열) 번호로 나눈 몫을 모두 더하면 된다. 그렇게 하게 되면 타겟보다 작거나 같은 수의 개수가 나온다. 예를 들어 아래를 보자.
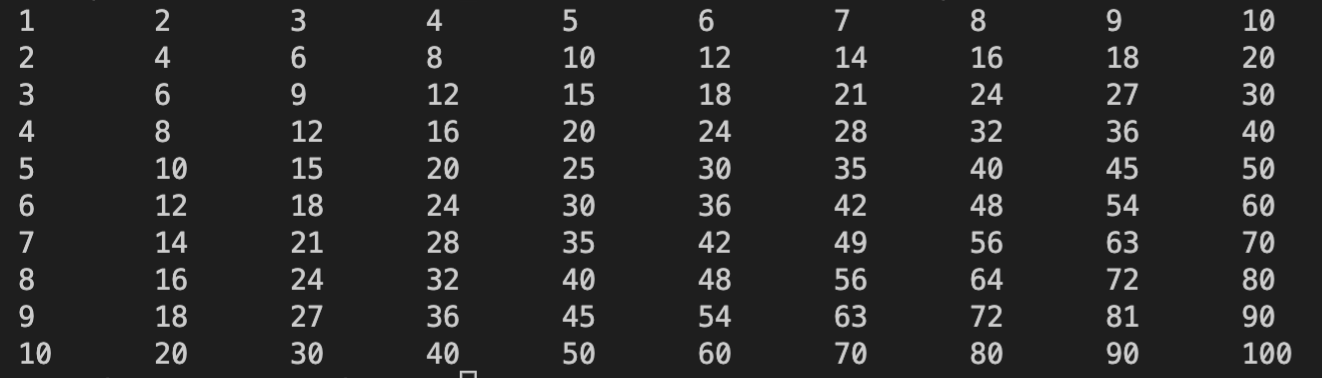
다음과 같은 배열에서 10 이하인 수의 개수를 구해보자. 10을 첫 번째 열 번호인 1로 나눈 몫은 10이고, 두 번째 열 번호인 2로 나눈 몫은 5이다. 이를 반복하면 10 + 5 + 3 + 2 + 2 + 1 + 1 + 1 + 1 + 1 = 27이다. 즉, 10 이하인 수의 개수는 27개이다.
마찬가지로 9 이하인 수의 개수는 같은 방법으로 구하게 된다면 9 + 4 + 3 + 2 + 1 + 1 + 1 + 1 + 1 + 0 = 23이다. 따라서 목표 인덱스가 24 ~ 27이라면 그 수는 10인 것이다.
각 열에서 나올 수 있는 개수는 최대 N개임에 유의해야 한다. 몫이 n보다 크게 되면 n만큼만 더하게 하기 위해서 min함수를 사용하였다.
풀이 및 코드
# 타겟 숫자의 위치(인덱스)를 리턴하는 함수
def locTarget(n, targetNum):
# 같은 수가 여러 개 있을 수 있음
# 최소 인덱스와 최대 인덱스를 리턴
minIdx = 0
maxIdx = 0
# 타겟 숫자를 각 열 번호로 나눈 몫이, 그 열에서 타겟 이하의 수의 개수임.
for row in range(1, n + 1):
# (타겟 - 1)보다 작거나 같은 수의 개수
minIdx += min((targetNum - 1) // row, n)
# 타겟보다 작거나 같은 수의 개수
maxIdx += min(targetNum // row, n)
return (minIdx, maxIdx)
def binarySearch(n, targetIdx, start, end):
mid = (start + end) // 2
minIdx, maxIdx = locTarget(n, mid)
# 이 조건을 만족한다면 정답
if (minIdx < targetIdx <= maxIdx):
return mid
# 타겟이 더 크다면 뒤의 배열을 다시 탐색
elif (targetIdx > maxIdx):
return binarySearch(n, targetIdx, mid + 1, end)
# 타겟이 더 작다면 앞의 배열을 다시 탐색
else :
return binarySearch(n, targetIdx, start, mid - 1)
n = int(input())
k = int(input())
print(binarySearch(n, k, 1, n ** 2))남들보다 두 배정도 느린 코드이길래 min, max를 구하던 것을 min인덱스만 구해서 그 인덱스를 저장하는 방식으로 구현해 보았는데 더 빠른 코드가 완성되었다.
# 타겟 숫자의 위치(인덱스)를 리턴하는 함수
def minIdx(n, targetNum):
idx = 0
# 타겟 숫자를 각 열 번호로 나눈 몫이, 그 열에서 타겟 이하의 수의 개수임.
for row in range(1, n + 1):
# (타겟 - 1)보다 작거나 같은 수의 개수
idx += min((targetNum - 1) // row, n)
return idx + 1
def binarySearch(n, targetIdx):
# 시작 인덱스는 1
start = 1
# 마지막 인덱스는 n 제곱
end = n ** 2
# 수를 저장하는 변수
num = -1
while (start <= end):
mid = (start + end) // 2
# 목표 인덱스가 최소 인덱스보다 크거나 같으면
if (minIdx(n, mid) <= targetIdx):
# 그 수를 저장 후
num = mid
# 다음 배열 탐색
start = mid + 1
else :
# 이전 배열 탐색
end = mid - 1
return num
n = int(input())
k = int(input())
print(binarySearch(n, k))
후기
이분 탐색으로는 전혀 생각이 나지 않았었는데, 풀이를 참고하니 풀렸다. 아직도 성장할 날이 한참 남은 것 같다.
'공부 > 백준' 카테고리의 다른 글
| [백준] 18353번 병사 배치하기 (Python) (0) | 2023.02.23 |
|---|---|
| [백준] 12015번 가장 긴 증가하는 부분 수열 2 (Python) (0) | 2023.02.17 |
| [백준] 2110번 공유기 설치 (Python) (0) | 2023.02.15 |
| [백준] 1654번 랜선 자르기 (Python) (0) | 2023.02.15 |
| [백준] 10816번 숫자 찾기 (Python) (0) | 2023.02.15 |
