정답 코드 및 풀이는 맨 아래에 있습니다.
https://www.acmicpc.net/problem/2293
- 다이나믹 프로그래밍은 전체적으로 구상이 매우 어려운 것 같다. 골드 5문제인데도 체감 난이도는 골드 1 정도 된다.
< 동전 1 >
[문제]
n가지 종류의 동전이 있다. 각각의 동전이 나타내는 가치는 다르다. 이 동전을 적당히 사용해서, 그 가치의 합이 k원이 되도록 하고 싶다. 그 경우의 수를 구하시오. 각각의 동전은 몇 개라도 사용할 수 있다.
사용한 동전의 구성이 같은데, 순서만 다른 것은 같은 경우이다.
[입력]
첫째 줄에 n, k가 주어진다. (1 ≤ n ≤ 100, 1 ≤ k ≤ 10,000) 다음 n개의 줄에는 각각의 동전의 가치가 주어진다. 동전의 가치는 100,000보다 작거나 같은 자연수이다.
[출력]
첫째 줄에 경우의 수를 출력한다. 경우의 수는 231보다 작다.
| 예제 입력 | 예제 출력 |
| 3 10 1 2 5 |
10 |
틀린 아이디어
dp[i][j]에 i원 동전보다 크거나 같은 것만 사용해서 j원을 만드는 경우의 수를 저장한다. i행의 동전의 가치를 x라고 한다면, dp[i][j]의 점화식은 다음과 같다.
dp[i][j] = dp[i][j - x] + dp[i + 1][j - x] + ... + dp[n][j - x]
다음 표를 보면 이해가 조금 쉽게 될 것이다. (행의 인덱스는 1부터 시작한다고 가정)

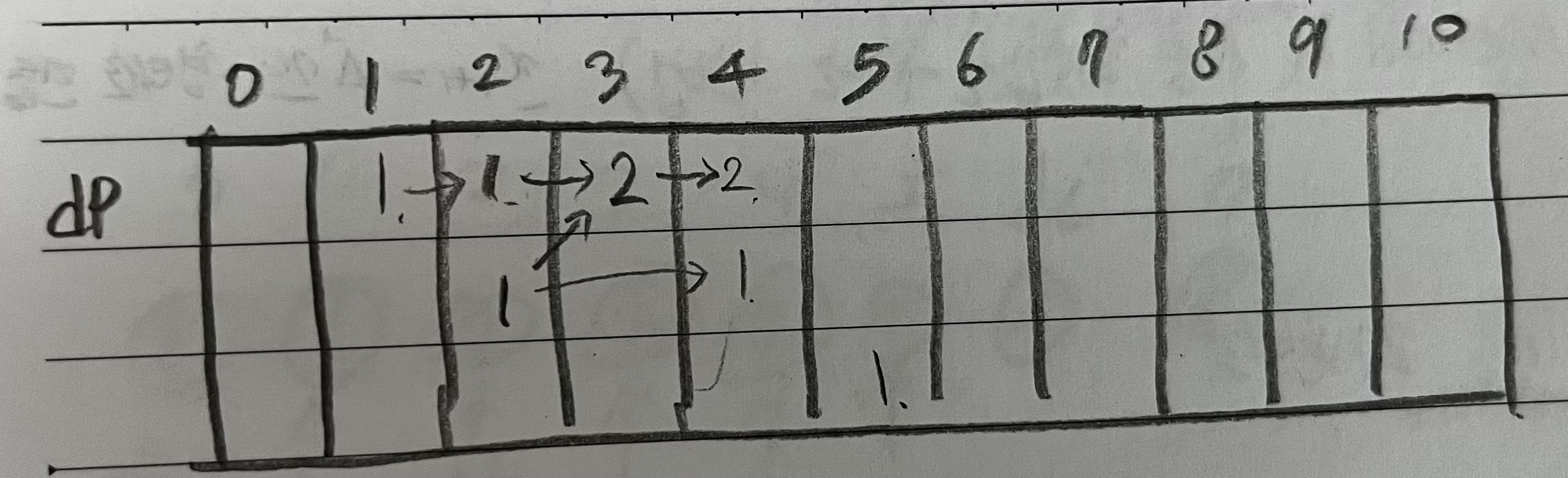
dp[1][2]는 dp[1][1]의 값을 그대로 받아 1이 된다. 이 때 dp[1][2]에서 센 경우는 "11"이다.
dp[1][3]는 dp[1][2] + dp[2][2]의 값인 2가 된다. 이때 dp[1][2] : "11", dp[2][2] : "2"이므로 dp[1][3]에서 센 경우는 "111", "12"이다.
같은 방식으로 dp[2][4]에 저장된 값은 dp[2][2]의 값을 물려받았기 때문에 "22"의 경우를 센 것이다.
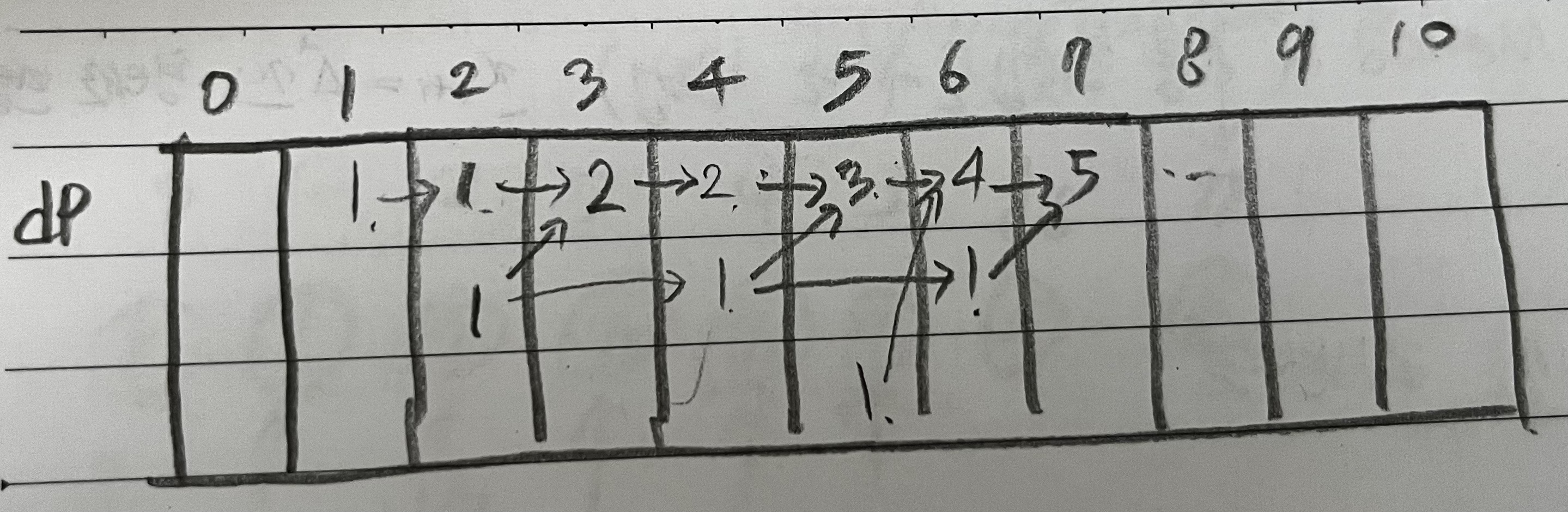
틀린 코드와 틀린 이유
import sys
input = sys.stdin.readline
def seekAnswer(dp):
ans = 0
for row in dp:
ans += row[-1]
return ans
n, k = map(int, input().split())
coins = sorted([0] + [int(input()) for _ in range(n)])
# n = 3, k = 10, coin = 1, 2, 5라고 하자.
# dp[i][j] : j라는 금액을 i 이상의 동전으로 만든 경우의 수 저장
dp = [[0 for amount in range(k + 1)] for coin in range(n + 1)]
# dp를 다음과 같이 초기화
# 1 0 0 0 0 0 0 0 0 0
# 0 1 0 0 0 0 0 0 0 0
# 0 0 0 0 1 0 0 0 0 0
for coinIdx in range(1, n + 1):
dp[coinIdx][coins[coinIdx]] = 1
for col in range(1, k + 1):
for row in range(1, n + 1):
coinValue = coins[row]
if (col - coinValue > 0):
# 현재 코인보다 크거나 같은 동전들의 dp값 모두 더함.
for i in range(row, n + 1):
dp[row][col] += dp[i][col - coinValue]
# dp 결과 :
# 1 1 2 2 3 4 5 6 7 8
# 0 1 0 1 0 1 1 1 1 1
# 0 0 0 0 1 0 0 0 0 1
print(seekAnswer(dp))결과는 예상한대로 아주 잘 나온다. 하지만 python3는 시간초과, pypy는 메모리 초과가 나게 된다. 이 알고리즘보다 더 효율적으로 코드를 짜야한다. 도저히 모르겠어서 다른 코드를 참고했다.
새로운 아이디어
dp를 2차원이 아닌 1차원으로 설정한다. 그리고 동전을 한 개씩 차례로 dp에 값을 업데이트해준다. 동전의 가치를 x라고 할 때 그 동전을 셀 때마다의 점화식은 다음과 같다.
dp[i] = dp[i] + dp[i - x]
전체적인 작동 구조는 다음과 같다.

풀이 및 코드
import sys
input = sys.stdin.readline
n, k = map(int, input().split())
coins = sorted([0] + [int(input()) for _ in range(n)])
# 0원을 만드는 경우의 수는 1가지이므로.
dp = [1] + [0] * k
for coin in coins:
for i in range(1, k + 1):
if (i >= coin):
dp[i] += dp[i - coin]
print(dp[-1])후기
생각하기 너무너무 어려운 문제들이 많았다. 이러한 문제들은 끊임없이 풀어보는 것 말고는 답이 없는 것 같다.
'공부 > 백준' 카테고리의 다른 글
| [백준] 18353번 병사 배치하기 (Python) (0) | 2023.02.23 |
|---|---|
| [백준] 12015번 가장 긴 증가하는 부분 수열 2 (Python) (0) | 2023.02.17 |
| [백준] 1300번 K번째 수 (Python) (0) | 2023.02.16 |
| [백준] 2110번 공유기 설치 (Python) (0) | 2023.02.15 |
| [백준] 1654번 랜선 자르기 (Python) (0) | 2023.02.15 |

