DFS(깊이 우선 탐색)은 그래프의 깊은 부분부터 탐색하는 알고리즘이다. DFS는 스택 자료구조나 재귀함수를 이용한다.
다음과 같은 과정으로 동작한다. 한 번 방문한 노드는 다시 방문하지 않으므로, 보통은 방문처리 리스트를 만들어 그 안에 False인지 True인지를 체크하는 방식으로 방문 여부를 파악한다.
- 스택에 시작 노드를 넣고 방문처리한다.
- 스택의 최상단 노드에 연결된 노드 중, 아직 방문하지 않은 노드가 있다면 그 노드를 스택에 넣고 방문처리한다. 방문하지 않은 노드가 없다면 그 최상단 노드를 꺼낸다.
- 스택에 아무 것도 없을 때 까지(혹은 문제에서 주어진 답을 풀 때 까지?) 반복한다.
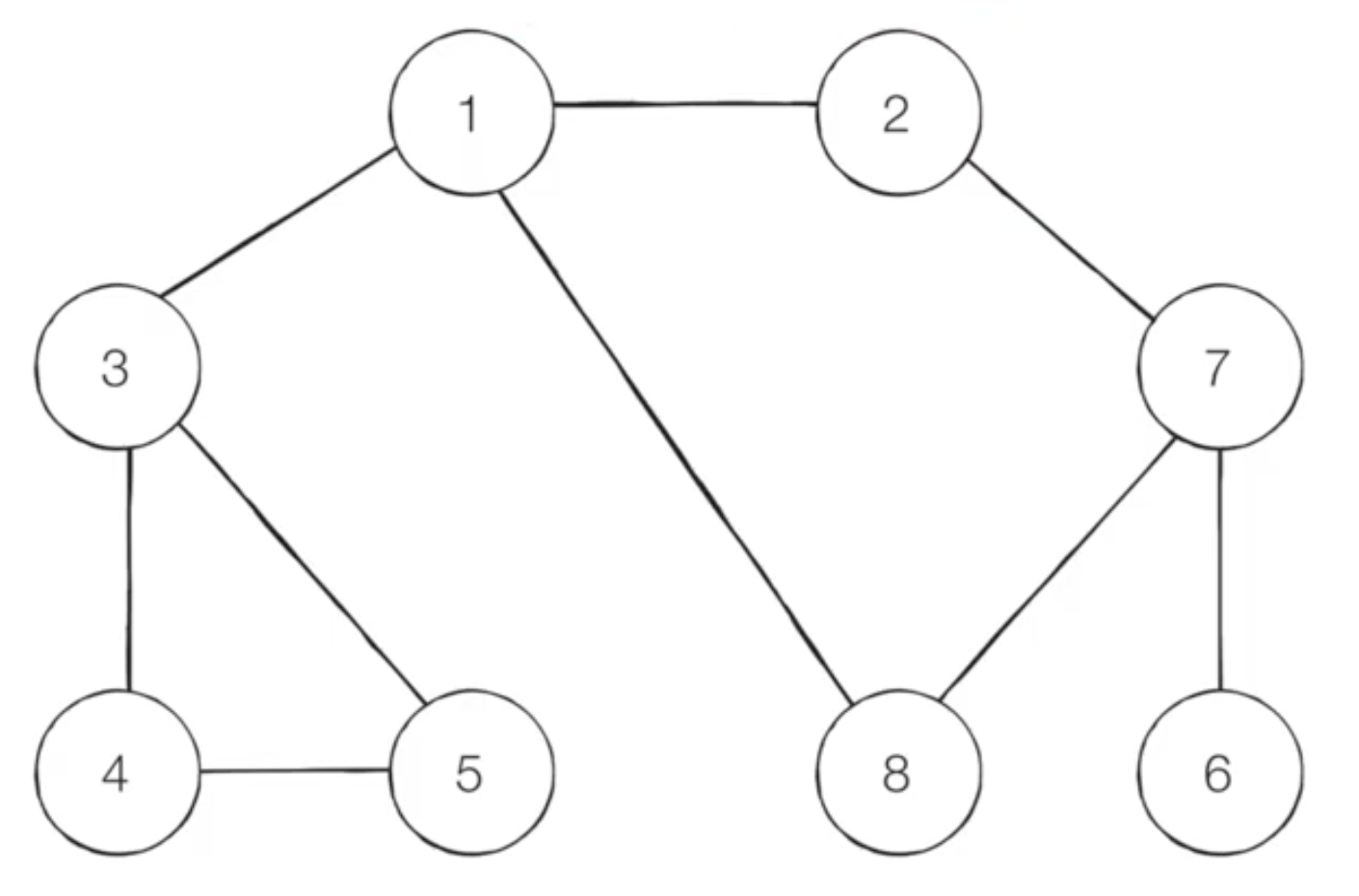
위와 같은 그래프가 있고, 시작노드는 1이며, 번호가 낮은 인접노드부터 방문한다고 하자.
- 시작노드인 1을 방문처리하고 스택에 넣는다. 스택 : 1
- 1의 인접노드 중 가장 작은 2를 방문처리하고 스택에 넣는다. 스택 : 1-2
- 2의 인접 노드 중 아직 방문하지 않은 7을 방문처리하고 스택에 넣는다. 스택 : 1-2-7
- 같은 방식으로 6을 넣는다. 1-2-7-6
- 6의 방문하지 않은 인접노드가 없으므로 6을 스택에서 꺼낸다.(pop) 스택 : 1-2-7
- 같은 방식으로 8을 방문한다. 1-2-7-8
- 8의 방문하지 않은 인접노드가 없으므로 스택에서 꺼낸다. 스택 1-2-7
- 7도 마찬가지. 스택 : 1-2
- 2도 마찬가지. 스택 1
- 이러한 방식으로 3, 4, 5도 방문한다.
- 마지막으로 1에도 더 이상 방문할 노드가 없으므로 스택에서 꺼내면 스택은 비게 된다.
- 탐색 순서 : 1 - 2 - 7 - 6 - 8 - 3 - 4 - 5
이 과정을 코드로 구현해보면 아래와 같다.
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
stack = []
stack.append(1)
visited[1] = True
while stack:
for node in graph[stack[-1]]:
if visited[node]:
continue
else :
visited[node] = True
print(node, end=' ')
stack.append(node)
break
else :
stack.pop()
# 2 7 6 8 3 4 5노드는 보통 1부터 시작하므로 그래프 리스트의 첫 번째 요소는 사용하지 않는 것이 일반적이다. 스택이 비어있지 않다면 계속 반복하여 실행해준다. 스택의 최상단 노드의 인접 노드를 크기 순서대로 접근해보며 아직 접근하지 않은 노드이면 방문처리 및 스택에 넣는 과정을 실행해준다. 2 7 6 8 3 4 5 순으로 위와 같은 순서를 출력한다.
하지만 일반적으로 DFS는 스택 대신 재귀함수로 구현하는 경우가 많다. 재귀로 구현한 코드는 아래와 같다.
def dfs(node):
print(node, end = ' ')
for adjNode in graph[node]:
if not visited[adjNode]:
visited[adjNode] = True
dfs(adjNode)
graph = [
[],
[2, 3, 8],
[1, 7],
[1, 4, 5],
[3, 5],
[3, 4],
[7],
[2, 6, 8],
[1, 7]
]
visited = [False] * 9
# 시작노드 방문 처리
visited[1] = True
dfs(1)인자로 들어온 노드의 인접 노드를 돌아보면서 아직 방문하지 않은 노드가 나오면 바로 방문해준다. 그렇게 되면 할 일이 다 끝나고 함수가 끝난다면 다른 인접노드로 들어가게 된다. 호출된 재귀함수도 스택이라는 공간에 담기는 것 이므로 위의 스택을 이용한 코드와 같은 동작을 하게 되는 것이다.
이제 문제를 풀어보자 ~
'공부 > 이것이 코딩테스트다' 카테고리의 다른 글
| DFS - 음료수 얼려 먹기 (0) | 2023.01.18 |
|---|---|
| BFS 이론 (0) | 2023.01.18 |
| 알고리즘을 배우는 이유 및 커리큘럼 (0) | 2023.01.03 |
| 구현 - 게임 개발 (0) | 2023.01.03 |
| 구현 - 왕실의 나이트 (0) | 2023.01.03 |

